Experts and scholars verify the accuracy of the sound absorption data measured using the SONOCAT device!

SoundInsightExperts and scholars from the company use SONOCAT equipment to measure the sound absorption coefficient of materials on-site, revealing the principles behind the measurement of the sound absorption coefficient of materials using SONOCAT equipment.

First, we need to understand what the sound absorption coefficient of a material is:

The surface sound absorption coefficient is defined as the ratio of active (net) sound power to incident sound power:

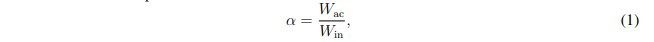
Where Wac and Win are the active and incident sound powers, respectively. Both powers can be calculated by integrating their related intensities over the surface:

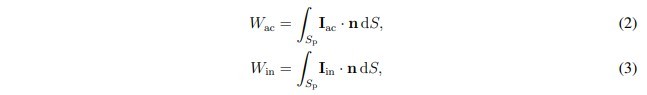
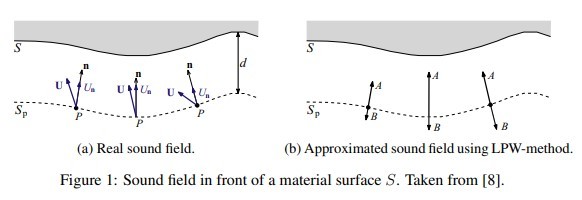
Where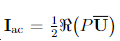is the active (net) sound intensity vector, P is the complex sound pressure, U is the conjugate of the complex particle velocity vector, and n is the normal vector pointing to the surface Sp, as shown in Figure 1 a. I_inis the incident sound intensity vector, which equals the active sound intensity vector for a fully absorbing surface. The active sound intensity vector normal to the surface can be easily measured using any pu or pp probe. However, it is impossible to determine the incident sound intensity vector in an unknown sound field. So, how does the local plane wave method adopted by SONOCAT achieve this?

Next, let's understand the LPW - Local Plane Wave method:

The LPW method is based on the local plane wave assumption, where the normal component of the sound field at each spatial coordinate is approximated by incident and reflected plane waves, as shown in Figure 1 b. Using e^iωtConvention, that is, p(r, t) = ℜ{P(r, ω)e^iωt}, the complex sound pressure P and the normal complex particle velocity Un = U·n can be written as:

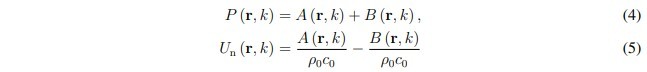
Where r is the position vector, k = ω/c0 is the wave number, A and B are the complex amplitudes of the incident and reflected waves, respectively, and ρ0c0 is the characteristic impedance. Note that we have omitted e^-ikzand e^ikzexponents by choosing z = 0 (where z is the local coordinate axis aligned with the normal vector n(r)). From this assumption, the normal incident and reflected intensities can be derived:

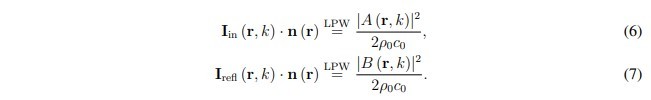
Additionally, the normal active intensity can also be expressed in terms of A and B:

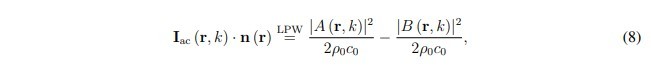
Thus, the normal active intensity equals the normal incident intensity minus the normal reflected intensity. Therefore, if A and B can be determined, the incident and active intensities can be found by evaluating equations (6) and (8), and the sound absorption coefficient can be calculated based on equations (1), (2), and (3). Using a pu probe, A and B in equations (4) and (5) can be easily solved. Next, let's use 1D and 3D pp probes to determine A and B.

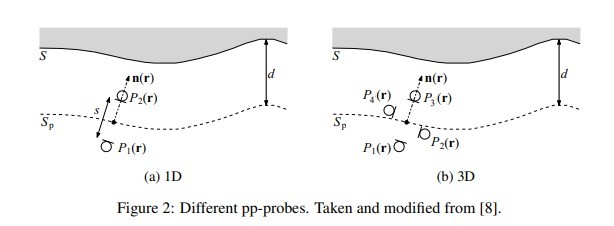
1D and 3D pp probes (see Figure 2) are typically used to determine the (normal component) active sound intensity vector using the well-known finite difference method. The sound pressure and particle velocity estimated at the midpoint of the probe can be used to apply the LPW method as explained in section 2.2. However, different (more intuitive) formulas can also be derived. For a 1D pp probe with two microphones spaced a distance s apart (see Figure 2 a), the LPW method can be written as [8]:

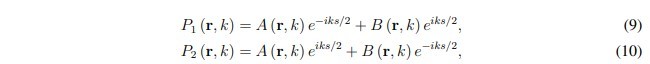
Where P1 and P2 are the measured microphone pressures. Solve the above equations to determine A and B, thereby determining the sound absorption coefficient according to the process specified at the end of section 2.2. For a 3D pp probe (see, for example, Figure 2b), the following system of linear equations should be solved:

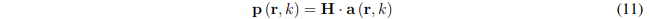
Where

Where P1 ... PM are the microphone pressures measured at positions z = z1 ... zM, with M≥4 being the number of microphones. Remember, z is the local coordinate axis aligned with the normal vector n(r), and z = 0 at r. The linear equations are solved in the least squares sense to obtain:

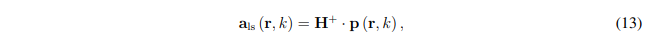
Where

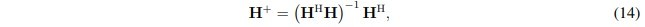
Where H denotes the conjugate transpose (or Hermitian conjugate). The least squares solution minimizes the sum of the squares of the residuals of the microphone signals. These residuals can be measurement noise, which encourages the use of multiple microphones. Solve equation (13) to determine A and B, thereby determining the sound absorption coefficient according to the previously specified process.

The above theoretically confirms that the local plane wave method can achieve on-site measurement of the sound absorption coefficient of materials.SoundInsightExperts and scholars from the company also conducted digital simulations (as shown in Figure 3) and experiments (using impedance tubes and SONOCAT for measurements, specifically referring to Figures 4, 5, and 6) to verify the accuracy of the on-site measurement of the sound absorption coefficient of materials using SONOCAT equipment.

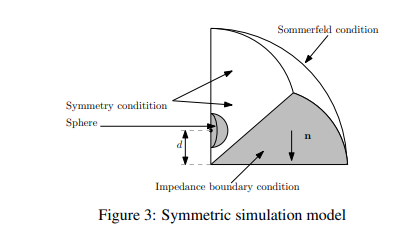
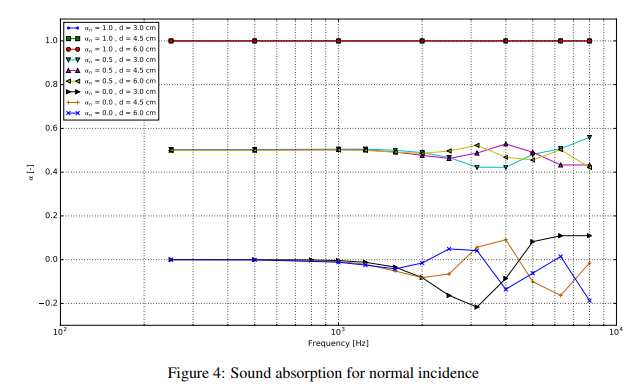
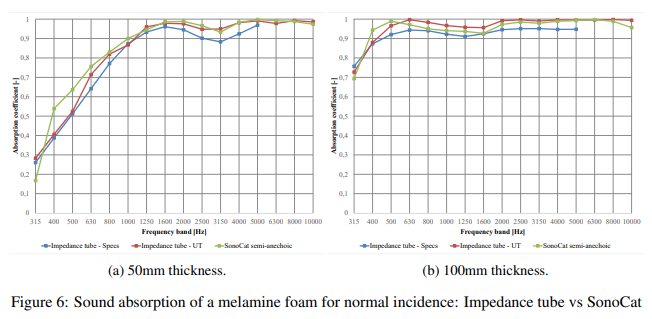
In the experiments, the normal incidence sound absorption coefficients of two different thicknesses (5 and 10 cm) of melamine resin foam samples were measured using SonoCat and the impedance tube from Twente University. The impedance tube measurements were conducted according to ISO 105342:2008. The SonoCat measurements were performed in a room with sound-absorbing characteristics above 300 Hz to avoid unnecessary reflections, as seen in Figure 5. A plywood backing material with a thickness of about 1.5 cm was used, and the distance d from the sphere to the surface was approximately 3 cm. A single cone speaker was placed about 1.5 meters above the SonoCat, emitting broadband white noise. It is assumed that the speaker is far enough from the surface so that the emitted sound waves have become plane waves above 300 Hz. The measurement results are shown in Figure 6, which, along with the material specifications provided by the manufacturer, generally show good matching of all sound absorption curves for each material thickness. Even for the impedance tube measurements, there are differences between all curves, but they are small. The general trend of each curve is comparable. For example, the "drop" around 3 kHz in Figure 6 a appears in all three curves. This indicates that the SONOCAT, using the LPW method, is reliable for on-site measurement of the sound absorption of material surfaces.